ESTIMACIÓN DE ERRORES EN LAS MEDIDAS
Dado que el valor de las magnitudes físicas que intervienen en una experiencia dada obtenidas por medida, bien directa o bien indirecta (por medio de los valores medidos de otras magnitudes ligadas con la magnitud problema mediante una fórmula física) viene siempre afectado de imprecisiones (imperfecciones del aparato de medida, o a las limitaciones impuestas por nuestros sentidos), debe aceptarse el hecho de que no es posible conocer el valor exacto de ninguna magnitud. Cualquier resultado numérico obtenido experimentalmente debe presentarse siempre acompañado de un número que indique cuánto puede alejarse este resultado del valor exacto. El principal objetivo de la denominada teoría de errores consiste en acotar el valor de dichas imprecisiones, denominadas errores experimentales.
CLASIFICACIÓN DE LOS ERRORES
El error se define como la diferencia entre el valor verdadero y el obtenido experimentalmente. El origen de los errores está en múltiples causas y atendiendo a éstas los errores se pueden clasificar en errores sistemáticos y errores accidentales.
Errores sistemáticos son errores que se repiten constantemente en el transcurso de un experimento. Afecta a todas las mediciones de un modo definido y es el mismo para todas ellas. Las causas probables pueden ser: errores instrumentales (de aparatos), errores personales, error de la elección del método.
Errores accidentales son variaciones que aparecen entre observaciones sucesivas realizadas por un mismo operador. No existe una causa predeterminada para este tipo de errores siendo incontrolables para un observador. Alteran la medida realizada tanto por exceso como por defecto. El origen de estos errores accidentales puede ser el cambio durante el experimento de las condiciones en el entorno, errores de apreciación del observador, errores de precisión del aparato de medida, etc.
EXACTITUD, PRECISIÓN Y SENSIBILIDAD
La exactitud de un aparato de medida se define como el grado de concordancia entre el valor verdadero y el experimental.
La precisión hace referencia a la concordancia entre una medida y otras de la misma magnitud.
La sensibilidad de un aparato está relacionada con el valor mínimo de la magnitud que es capaz de medir. Normalmente, se admite que la sensibilidad de un aparato viene indicada por el valor de la división más pequeña de la escala de medida.
ERROR ABSOLUTO Y ERROR RELATIVO
Si medimos una cierta magnitud física cuyo valor "verdadero" es z*, obteniendo un valor de la medida z, llamaremos error absoluto Δz en dicha medida, a la diferencia z – z*. El error absoluto nos da una medida de la desviación, en términos absolutos respecto al valor "verdadero".
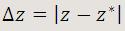
No obstante, en ocasiones nos interesa resaltar la importancia relativa de esa desviación. Para tal fin, se usa el error relativo. El error relativo εr se define como el cociente entre el error absoluto y el valor "verdadero". En forma porcentual se expresará multiplicado por cien.
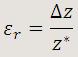
Para una magnitud física dada, la teoría de errores proporciona un método matemático para calcular con buena aproximación cuánto puede alejarse el valor medio experimentalmente del valor verdadero.
El resultado experimental para una magnitud z lo expresamos como:
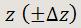
Siendo z el resultado experimental de una medida y Δz el resultado experimental de la misma.
Distinguiremos dos situaciones: medida directa y medida indirecta.
Medida directa de una magnitud física
El procedimiento para establecer el resultado de la medida y su error correspondiente no será el mismo si se hace una sola medida de la magnitud física que si se hacen varias medidas. En principio, cualquier medida experimental debe ser repetida varias veces. Sólo en el caso de que se observe que el resultado obtenido es siempre idénticamente el mismo, y sólo en ese caso, estará justificado el quedarse con una sola medida.
Supongamos que z1 sea el valor experimental de una medida obtenida para z. Como error absoluto, Δz, se adoptará:
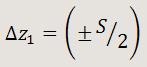
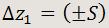
Ejemplos:
(a) Supongamos que un amperímetro analógico (medidor de intensidad de corriente) tiene una escala de lectura que aprecia hasta décimas de amperio (sensibilidad: S=0.1 A) y, al hacer una medida, la aguja se queda a la mitad de camino entre 0.6 A y 0.7 A. En ese caso, se podrá tomar como valor experimental z1 = 0.65 A y como error absoluto 0.1/2 = 0.05 A. Se dirá que la intensidad de corriente es de 0.65 (±0.05) A.
(b) Supongamos que un cronómetro digital que mide hasta milésimas de segundo (sensibilidad: S = 1 ms) estima el período de oscilación de un péndulo en 882 milisegundos. Entonces z1 = 882 ms y el error absoluto es de 1 ms. El resultado se dará como 882 (±1) ms.
Medida indirecta de una magnitud física
Cuando se utiliza una fórmula para calcular magnitudes a partir de otras que se han medido directamente y a partir de constantes físicas, decimos que estamos realizando una medida indirecta. En algunas ocasiones, una magnitud física es medida indirectamente a partir de otra/s magnitud/es. Cada una de estas otras magnitudes, viene afectada por un margen de error.
Supongamos que y sea una magnitud que va a ser medida indirectamente mediante una fórmula a partir de otras magnitudes x1, x2,...,xn que han sido medidas directamente y que tienen como errores absolutos Δx1, Δx2,...,Δxn, respectivamente.
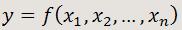
Entonces podemos obtener una aproximación para el error absoluto Δy en función de los errores absolutos de las variables directas:
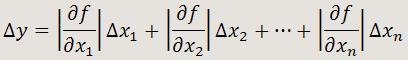
Escribiremos por tanto, como resultado:
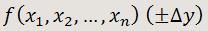
Ejemplos:
(a) Supongamos que se ha medido una magnitud física x obteniéndose un valor experimental 0.442 (±0.002) y que tenemos interés en medir indirectamente otra magnitud física que es precisamente y = x2. En primer lugar, el valor experimental de y es y = (0.442)2 = 0.195. El error absoluto de y se calculará de la siguiente forma:
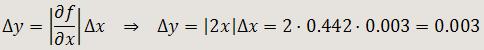
Por tanto, el resultado experimental es: y = 0.195 (±0.003)
(b) Supongamos que se ha medido de forma directa la tensión (con un voltímetro) y la intensidad (con un amperímetro) en una resistencia obteniéndose V = 10.0 (±0.1) V e I = 2.50 (±0.05) A. Determinaremos el valor de R = V/I (ley de Ohm) con su error.
Dado que R se calcula a partir de otras dos magnitudes que se han medido directamente, es decir, R = R(V,I) = V/I, obtendríamos lo siguiente:
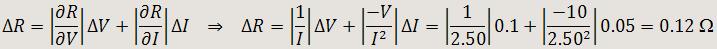
El valor experimental de R se calcula por aplicación directa de la ley de Ohm: R = V/I = 10/2.50 = 4.00 Ω
Por tanto R = 4.00 (±0.12) Ω
PRESENTACIÓN DE RESULTADOS NUMÉRICOS
Cualquier valor experimental z de una magnitud física debe expresarse con un determinado número de cifras, que viene limitado por el valor del error absoluto. El número de cifras que hay desde la primera cifra distinta de cero empezando por la izquierda hasta la primera cifra que venga afectada por el error absoluto, ambas inclusive, es el número de cifras significativas del resultado. Es evidente que no tiene sentido escribir cifras no significativas de un resultado. Además, el convenio de sólo escribir las cifras significativas de un resultado nos hace tener información inmediata sobre su error absoluto por el mero hecho de verlo escrito.
El expresar un resultado en una u otra unidad no cambia su número de cifras significaticvas. Por eso, los ceros a la izquierda de un número no son cifras significativas y sólo se utilizan para situar el lugar decimal. Los ceros a la izquierda pueden evitarse usando notación científica.
Ejemplo:
Decir que una masa es de 2.342 g o decir que es de 0.002342 Kg, no cambia el número de cifras significativas que en ambos casos es 4. En notación científica se escribiría 2.342·10-3 Kg.
Tras obtener el error absoluto, será necesario, por tanto, llevar a cabo un redondeo en el valor de la medida para conservar sólo cifras significativas.
Finalmente, hay que especificar cómo se aplica el redondeo a la propia expresión del error absoluto. Debido al significado de incertidumbre en el resultado que se asocia al error absoluto, éste mismo no debe expresarse nunca con más de dos cifras. Por convenio, error absoluto se expresa con dos cifras si la primera de ellas es un 1 o, si siendo un 2, no llega a 5 la segunda. En los demás casos, el error absoluto deberá expresarse con una sóla cifra obtenida mediante redondeo.
Ejemplo:
| INCORRECTO | CORRECTO |
| 5.619 (±0.126) | 5.62 (±0.13) |
| 8.4 (±0.06) | 8.40 (±0.06) |
| 345.233 (±0.18) | 345.23 (±0.18) |
| 2.023 (±0.0261) | 2.02 (±0.03) |
Es de vital importancia conocer los errores absolutos de las medidas de las magnitudes físicas a la hora de obtener conclusiones científicas.
Ejemplo:
Supongamos que se desea determinar si la temperatura T tiene algún efecto sobre la resistencia eléctrica de una bobina de alambre de cobre. Se miden dos valores de la resistencia R para dos temperaturas distintas y se obtiene:
| T1 = 20ºC | R1 = 4.024 Ω |
| T2 = 30ºC | R2 = 4.030 Ω |
Sin los errores absolutos para cada valor de la resistencia no podemos sacar conclusiones científicas. Si el error de cada medida es de 0.002, entonces podemos concluir que la resistencia eléctrica aumenta con la temperatura T. En cambio, si el error fuese de 0.008 entonces no tenemos bases para llegar a la misma conclusión.
REPRESENTACIÓN DE DATOS EXPERIMENTALES
Funciones lineales
Son aquellas funciones cuya representación gráfica es una recta. Todas estas funciones admiten una expresión analítica que toma la siguiente forma:
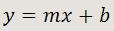
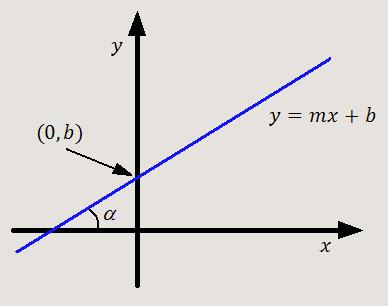
En una recta de ecuación y = mx + b, se llama pendiente al número m y es la tangente del ángulo α que forma la recta con la horizontal (Oº < α < 180º). Al número b se le llama ordenada en el origen, y representa el punto de corte de la recta con el eje Y, concretamente, en el punto (0, b).
Ajuste de la recta de regresión por el método de mínimos cuadrados
Con frecuencia, se plantea el problema de encontrar una expresión matemática del tipo y = f(x), de la ley física que rige el comportamiento de un determinado fenómeno, a partir de una serie de N medidas (xi, yi), de las magnitudes x e y que lo caracterizan. Cuando la representación gráfica del fenómeno estudiado proporciona una distribución de los puntos experimentales en forma prácticamente lineal, es conveniente determinar la ecuación de larecta que será expresión de la ley física que rige el fenómeno estudiado, utilizando para ello el método de mínimos cuadrados. Dicha recta debe cumplir la condición de que los puntos experimentales, queden distribuidos simétricamente a ambas partes de la misma, y además, lo más próximos posible. Esta condición se cumple si se obliga a que la recta de ecuación y = mx + b cumpla que la siguiente expresión tenga un valor mínimo:
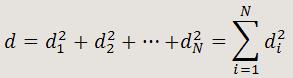
Donde
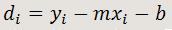
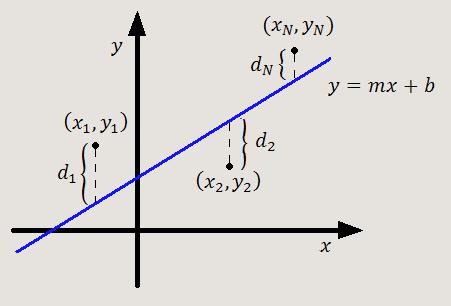
Por tanto, la expresión a minimizar será:
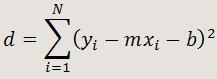
Derivando d respecto a m y b, y anulando ambas derivadas, tras una serie de operaciones se obtiene:
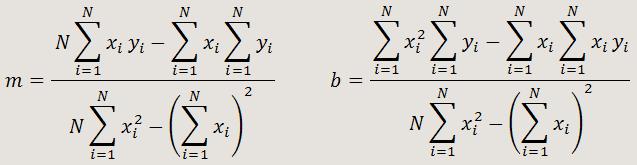
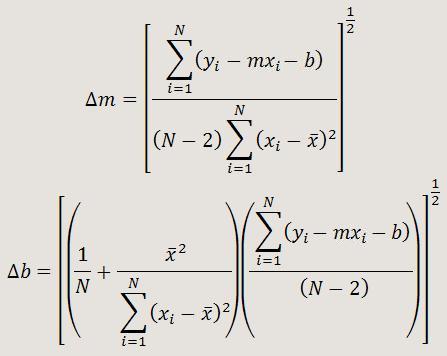
Las expresiones correspondientes al cálculo del error de la pendiente y el error de la ordenada en el origen son:
Además de los valores de la pendiente y la ordenada en el origen, es interesante obtener el denominado coeficiente de correlación lineal r, que nos da una medida del grado de correlación entre los valores de las variables x e y, es decir, hasta qué, punto x e y están relacionadas mediante una función lineal. Varía entre 0 (no existe correlación) y ±1 (correlación completa). La expresión de r es: